Ball Bouncing Challenge

Ball Bouncing

On Saturday, Christina and I took a stroll down to the gym to test the velocity and position of a Champion basketball after bouncing it.  

To further help you visualize our collection of data, here's a video of Christina bouncing the ball:

This is what the video looked like with the data points:

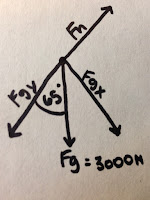
Here's a free body diagram of what the ball looked like in the air:

The reason why there are no other forces on the ball is because only the force of gravity is pulling the ball to the earth.

Here's our v v.s. t graph:

On our v v.s. t graph, we were observing two things: the ball's velocity in the vertical direction and the balls' velocity in the horizontal direction.  The data with the light blue border corresponds with the light purple line on the graph.  This line was a representation of the ball's velocity in the horizontal direction.  It is basically a straight line, only a bit of air resistance was slowing it down.  The data with the pink border corresponds with the green line, which depicts the ball's vertical velocity.  As you can see, when the ball hit the ground, it's velocity was at 0, but then increased in the negative direction as it continued on to another bounce.

Here's our x v.s. t graph:

In this graph, you can see how the ball's vertical movement gave us a parabola, showing that it had an acceleration.  The ball's horizontal line showed that the ball moved forward at constant velocity.

Analysis

The acceleration in the y direction was -9.6 m/s^2 (which would make sense, as the average force of gravity is 10N).  This was the slope of our green line in the v v.s. t graph.The acceleration in the x direction was -0.54 m/s^2.  This was the slope of the purple line in the v v.s. t graph.  

The initial velocity in the horizontal direction was about 6 m/s, and the initial velocity in the vertical direction was about 4.6 m/s (the graph is a little bit off, but our data is correct).

The ball's velocity at the top of it's path in the horizontal direction was constant, as no forces (except for minor air resistance) prevented it from moving forward.  The ball's velocity at the top of it's path in the vertical direction was also 0, and you know this because it had been slowing down until it had reached it's peak, where it stopped momentarily before accelerating to the floor.

The final velocity in the vertical direction was about -5 m/s, and the final velocity in the horizontal direction remained at a constant 6 m/s.

The ball's highest point was 2 meters, as represented on our graph of x v.s. t.  In order to solve for the distance travelled in the horizontal direction, you can use:

Δx= 1/2 a t^2 + vi * t

By plugging in -0.54 as the acceleration, 1.05 as the time, and 6 as the initial velocity, you end up with the Δx being 6.01 meters.

It took the ball 0.6 seconds to reach the peak of it's bounce.  The ball was in the air for 1.1 seconds, which is shown on out x v.s. t graph.  

Conclusions

The experiment was pretty impressive, as we studied the balls' motion not only in the forward direction, but in the upward direction as well.  The vertical acceleration was almost equal to the force of gravity, which is 9.8N (or 10N).  The horizontal acceleration however was irrelevant, because the ball bounced at a constant velocity of 6 m/s across the gym.  This justifies that the ball's upwards velocity was not constant, but it's forwards velocity was.  

We solved for the horizontal displacement by using the change in x formula.  By plugging in the acceleration, time, and initial velocity, we were able to conclude that the total horizontal displacement was 6.01 meters.  The ball's velocity at the top of it's path in the vertical direction was 0m/s, as it was changing from going up to going down.  It had been going in the upwards direction, slowing down in the process, until it vertically stops momentarily, and then continues accelerating in the downwards direction.  It's horizontal velocity however remained constant at 6 m/s, as the ball continued moving forward while it's vertical path had acceleration.  To solve for the vertical component, you would also use the 'change in x' formula, and plug in the total time.  However, to solve for the ball's height, you would use the 'change in x' formula, and plug in the amount of time it took to reach it's height. 

UFPM Challenge

UFPM Challenge

Group ~ Miranda, Will C, Robert

Our goal was to calculate the exact time it would take for the cart to reach the same spot of a hanging weight that was quickly dropping.  We found the total mass of the system, which was .639kg (rounded to .64kg), and used that to find the acceleration.  

Here's a diagram of what our setup looked like:

We solved for the acceleration of the weight, enabling for us to solve for time later on.

To make it easier to understand the information, we drew a free body diagram of the system.

  We measured that the distance the weight would have to travel to reach the ground, which was .74 meters, and we knew that the acceleration was .78 m/s2.  Thus, we used our information to solve for the time it would take for the weight to reach the floor.

We already solved for the acceleration of the weight, so then we had to solve for the acceleration of the cart.  We measured that it took 3.6 seconds for the cart to move 1 meter, meaning it had a velocity of .28 m/s.  Therefore, we had to find the distance it would travel in the same amount of time it would take for the weight to hit the floor. 

This information meant that we had to position the cart .38 of a meter away from where the weight would hit the floor.  By releasing the cart from this distance and the weight from its height at the same time, they would potentially collide.  

Our hypothesis was correct!  When we released the cart and the weight at the same time, the weight landed in the center of the cart.  We had no percent error, because our time was exactly what we had predicted.

If you want to see our success, go to https://youtu.be/P3dvTJU3kcU 

Unit 4 - Unbalanced Force Particle Model

Skateboard Challenge

Initial Trends and Patterns:

- The object accelerates when more force is applied

- The more force you apply, the faster it accelerates.  The less force you apply, the slower it accelerates

- The lighter the object is, the faster the acceleration (and vice versa pertaining to heavy objects)

- There's an inverse relationship between mass and acceleration

- There's a direct relationship between force and acceleration

Elevator Challenge Question

An elevator is moving up at constant velocity of 2.5 m/s.  The passenger has a mass of 85kg.

The elevator now accelerates upwards at 2m/s^2.

What's the equation of the vertical forces on the passenger?

Fnet = Fg + Fn

Newton's 2nd Law Key Points:

Situation - You have a 2kg box being pushed with a net force of 4N.

1) Calculate the box's acceleration:

a = Fnet/mass

a=4/2

a=2m/s^2

2) How would the acceleration compare if the mass of the box was cut in half?

The acceleration would increase/double.

3) How would the acceleration compare if the force was doubled?

The acceleration would increase/double.

4) How would the acceleration compare if the force was cut in half?

The acceleration would decrease/be cut in half.

5) How would the acceleration compare if the mass was doubled?

The acceleration would decrease due to no change in the force.

6) How would the acceleration compare if the mass and force was doubled?

The ratio would be higher between mass and force compared to the original, but essentially the object would be moving with the same acceleration.

7) How would the acceleration compare if the force and mass was cut in half?

The ratio would be lower between mass and force compared to the original, but the object would still move with the same acceleration.

8) How would the acceleration compare if the force was doubled and mass was cut in half?

The object would accelerate at a quick rate because a lot of force would be exerted on a light object.

9) How would the acceleration compare if the force was cut in half and the mass doubled?

The acceleration would decrease by a lot, because not a lot of force would be exerted on a heavier object.

Practice Problems!

1) A race car has a mass of 710kg.  It starts from rest and travels 40 meters in 3 seconds.  How big is the net force on the car?

First, solve for the acceleration.  Plug in all of the variables you have:

When you find the acceleration, solve for the Fnet.  This will be the total force acting on the car:

Here's what a force diagram would look like: 

2) A rollercoaster car has a mass of 300kg with passengers.  It accelerated down a 65 degree hill.  Draw a force diagram, determine the gravitational force parallel to the hill, and find the acceleration.

3) A sled weighing 300N is moved at constant velocity over a horizontal floor by a push force of 50N.  Determine the coefficient of kinetic friction between the sled and the floor.  Then, determine the sled's acceleration if the kinetic friction was 0.

Formulas to be familiar with:

vf = at + vi

Δx = 1/2 aΔt^2 + viΔt

vf^2 = vi^2 + 2aΔx

a = Δv/Δt

a = Fnet/mass

Ffriction = µ (Fnormal)